Infinite training with infinite networks

What happens to a neural network when its size goes to infinity? Despite the strangeness of the question, the answer turns out to be a fascinating one: the network converges to a so-called Gaussian Process (GP). In this article we overview some recent, notable results exploring the connections between the two, most importantly the neural tangent kernel (NTK). We also introduce a JAX library, Neural Tangents, to compute the predictions of such an infinite neural network in the general case!

A brief introduction to Gaussian Processes

Gaussian Processes (GPs) are one of those Bayesian techniques that one either loves or hates (or, maybe, simply finds confusing). If you have been around for a while, there is a good chance that you were introduced to the topic by the classic book from Williams and Rasmussen.¹ Otherwise, you might have stumbled upon the beautiful Distill article devoted to them.

A GP is a way to specify a probability distribution over functions, which makes them especially attractive whenever you want to deal with uncertainty. You probably already know how to define probabilities over real numbers (random variables) and over vectors (again, random variables, even if we usually call them random vectors). Now we want to introduce a probability measure over an infinite-dimensional space: for example, the space $L^2([0,1])$ of square-integrable functions over $I=[0,1]$. Things get complicated, for reasons which are probably best left in a footnote ² 😜. Fascinatingly, a GP solves the complication by making only two assumptions:

1. for any set of points $S_n=\{x_1,\dots,x_n\}$ belonging to the domain of our function, the corresponding function values $f(x_1),\dots,f(x_n)$ have a joint Gaussian density.
2. (this one is a more technical assumption that you might skip on first reading) given two sets of points $S_m$ and $S_n$ such that $S_m \subset S_n$, the two joint Gaussian densities $p_m(f_1,\dots,f_m)$ and $p_n(f_1,\dots,f_m,\dots,f_n)$ are consistent, i.e.,

\[ \int_{\mathbb{R}^{n-m+1}}p_n(x_1,\dots,x_{m},x_{m+1},\dots,x_n)\text{d}x_{m+1}\dots \text{d}x_n=f_m(x_1,\dots,x_m)\]

By the Kolmogorov extension theorem, just these two properties guarantee that we defined a consistent distribution over functions, i.e., a stochastic process. You can specify a GP completely by describing the mean of this probability distribution (generally, zero), and its covariance. The covariance describes the correlation existing between two different points: for example, if you suppose that two points spaced at a certain distance are heavily correlated (say, in financial trends), you can embed this knowledge inside the covariance function.

The values of the covariance are represented through a kernel function, which you might remember from other algorithms, such as Support Vector Machines (SVMs), or kernel PCA. In this case, you will have seen, for example, the exponential kernel:

$$ \kappa(x_1, x_2) = \exp\left\{ \frac{\lVert x_1 - x_2 \rVert^2}{l}\right\}$$

There is a beautiful algebra correlated to manually designing kernels, which powers several branches in machine learning. The key concept is that, by specifying this kernel, and conditioning on the training data, the GP allows to obtain entire distributions over functions, which is infinitely more expressive than a single function (as done, for example, in neural networks).

Again, you HAVE TO read the Distill blog and see it visually.

I want my neural networks back!

Sorry.

Ok, here we go: consider a neural network with a single hidden layer and one output, of which you initialize all weights from a Gaussian distribution with mean zero and a certain standard deviation. Each weight can be seen as an i.i.d. variable, and because the output is a weighted sum, by the Central Limit theorem it will converge to a Gaussian distribution once you increase the hidden layer's width.

In fact, in the limit of infinite width, the neural network converges exactly... to a GP! The GP is fully described by a zero mean and by a kernel with a simple form:

$$ \kappa(x_1, x_2) = \mathbb{E}\left[f(x_1)f(x_2)\right] \,,$$

where $f(x)$ is the neural network, and the expectation is taken w.r.t. all possible weights. This notable result was obtained in the seminal PhD work from Neal,³ while an analytical form of the kernel for a single hidden layer neural network was derived by Williams.⁴

This result is more remarkable than it might sound: it allows to specify a neural network architecture, and then compute the predictions corresponding to an equivalent, infinite network!

Infinite deep networks are also GPs

While an extension to deeper networks was a common idea, only recently a number of papers have shown by induction that practically any neural network, once its widths are allowed to go to infinity, is equivalent to a GP.⁵ Even better, it is possible to provide a constructive process for computing the kernel of these GPs (we'll show how to implement this in the last section of the article; before, we take a detour on an even weirder application of the relation between neural networks and GPs).

Training networks for infinite time?

If this was all there is to the connection between NNs and GPs, it would be remarkable, but probably not enough to justify the amount of attention this theme has been receiving lately. However, it turns out that a lot can be obtained by considering a closely related kernel, the neural tangent kernel (NTK):

$$ \text{NTK}(x_1, x_2) = \left[\nabla f(x_1)\right]^T \nabla f(x_2) \,,$$

where the quantities represent the Jacobian of the network, i.e., their gradient w.r.t. all parameters. Why is this interesting? Consider performing gradient descent of the parameters $\theta$ of the network:

$$ \theta_{t+1} = \theta_t - \eta \nabla L(\theta_t) \,,$$

where $L$ is some loss and $\eta$ the learning rate. If we take smaller and smaller learning rates, the dynamics of this process are described by a differential equation:

$$ \dot{\theta_t} = -\nabla L(\theta_t)$$

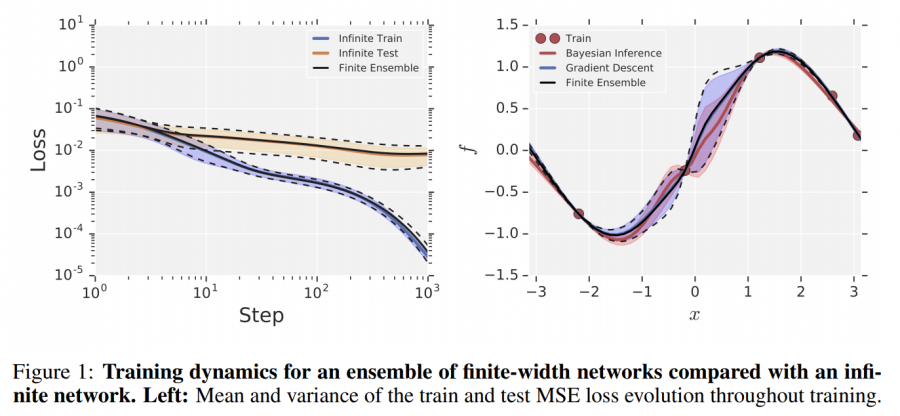
Fascinatingly, this expression can be exactly analyzed with some quantities involving the NTK!⁶⁷ This is not as useful as it may seems because, in general, the NTK changes in time according to the parameters of the network. However, it can be shown that in the infinite-width regime, the NTK stays constant, and the previous expression can be solved in closed-form, obtaining the predictions corresponding to a neural network trained... for infinite time!

If you are interested in a more formal, yet still accessible, derivation, there is a very nice blog post by Rajat Vadiraj Dwaraknath: Understanding the neural tangent kernel.

How can we use all this machinery in practice?

Introducing Neural Tangents

While this is all extremely interesting, actually computing the two kernels requires careful coding. In addition, exploiting them in a GP process requires to implement further code, and to handle a series of numerical and/or scaling problems.

Luckily, a small time ago Google released Neural Tangents, a JAX library that makes this process almost automatic. We highlight some key ideas here, but you can find a full demo of its use on a companion Colab notebook.

To begin with, recall how we can specify a neural network in JAX using the internal Stax library:

init_fn, apply_fn = stax.serial(
    stax.Dense(100), stax.Relu,
    stax.Dense(1)
)

JAX is mostly functional, so the neural network is described by one function for its initialization, and one function for gathering predictions.

The definition in NT is almost equivalent:

from neural_tangents import stax as stax_nt
init_fn, apply_fn, kernel_fn = stax_nt.serial(
    stax_nt.Dense(100), stax_nt.Relu(),
    stax_nt.Dense(1)
)

We are using the Stax implementation from NT (not from JAX): the only difference (apart from the fact that Relu requires a function call), is that we also obtain a third function kernel_fn, which allows to automatically make predictions with one of the two kernels seen before!

Let us see an example with the NTK:

from neural_tangents import predict
mean, var = predict.gp_inference(kernel_fn, X_train, y_train, X_test, \
        diag_reg=1e-3, get='ntk', compute_cov=True)

gp_inference performs GP inference using the kernel, and it can also use Monte Carlo approximations whenever the network does not admit a closed-form solution for the kernel. mean and cov and the mean and covariance of the predictions, which, as you recall, corresponds to an infinite-width network trained for infinite time!

We can also plot them: you can notice some small vertical bars, corresponding to predictions with a small amount of uncertainty.

Conclusion

There is a lot to go to from here: the papers linked below and in the NT repository are a good starting point in this ever-growing body of literature which has already reserved several surprises. Notably, it is still unclear how much the dynamics described by the NTK corresponds to the dynamics empirically observed in neural networks used in practice. Still, NT provides an extremely simple and practical way of playing around with infinite-width networks.

Acknowledgments

The author thanks Andrea Panizza for help in proofreading and for rewriting part of the description on Gaussian Processes.

References

Previous Post Next Post