Un mese fa si è conclusa la settima edizione della International Conference on Learning Representations (ICLR), una delle conferenze più prestigiose dedicate al mondo del deep learning. Come ogni edizione, grande interesse hanno destato i best paper award, elogi scelti da un comitato di prestigio per premiare articoli di particolare interesse o dal notevole impatto scientifico tra gli oltre 1500 sottomessi alla conferenza.
Due gli articoli premiati quest'anno. Ordered Neurons: Integrating Tree Structures into Recurrent Neural Networks, dall'Università di Montréal e Microsoft Research, esplora come forzare una rete neurale ricorrente ad apprendere rappresentazioni di tipo gerarchico, come ad esempio quelle presenti nella struttura grammaticale di una frase.
In questo breve post, però, vogliamo focalizzarci sul secondo articolo premiato: The Lottery Ticket Hypothesis, pubblicato da due ricercatori del MIT Computer Science & Artificial Intelligence Laboratory, propone una interessante ipotesi sul funzionamento delle reti neurali che, se verificata, promette di gettare nuova luce sul loro processo di allenamento e la possibilità di allenare reti estremamente più compatte di quelle comunemente usate finora.
Di seguito riportiamo una breve analisi di questa ipotesi, ed alcuni dei lavori più interessanti tra quelli che l'hanno ripresa, estesa, e discussa.
La Lottery Ticket Hypothesis, spiegata
Partiamo da una osservazione empirica: le reti neurali hanno, in generale, molti, molti più parametri di quanti sembrerebbero necessari. Alcuni tra i lavori più celebri nel campo del pruning (es., la Deep Compression) mostrano come sia relativamente semplice ridurre il numero di parametri di una rete, anche di un ordine di grandezza, senza andare ad intaccarne l'accuratezza.
Eppure, una seconda osservazione empirica è che cominciare l'allenamento con una rete di dimensioni già ridotte è altrettanto difficile: è invece necessario inizializzare una rete neurale più grande, e poi ridurne il numero di parametri con una o più tecniche durante o dopo l'allenamento.
La Lottery Ticket Hypothesis (LTH) cerca di spiegare questo apparente binomio, postulando che il successo di una singola rete neurale non dipenda dall'intera architettura, ma da una o più sotto-reti al suo interno, che gli autori chiamano lottery tickets (trad., biglietti della lotteria), o più semplicemente tickets. La difficoltà è che l'accuratezza dei tickets dipende non soltanto dal modo in cui sono collegati, ma anche dai valori che assumono all'inizializzazione, e che a loro volta ne semplificano o meno la fase di ottimizzazione.
Una rete neurale con molti strati contiene un numero esponenzialmente grande di questi tickets, definiti da tutti i modi in cui i vari neuroni possono collegarsi tra di loro. Questo aumenta moltissimo la probabilità di trovare almeno un ticket particolarmente buono per il problema che stiamo affrontando, ed è su quello che, in pratica, si concentra implicitamente la fase di ottimizzazione.
Secondo questa visione, quindi, allenare una rete neurale è una sorta di enorme lotteria dove la vittoria è quasi assicurata.
L'ipotesi è formulata in modo leggermente più tecnico all'interno dell'articolo originale (che vi consigliamo di leggere), ma questo basta a comprenderne i punti salienti.
A cosa può servire l'ipotesi?
Al di là di spiegare (seppur in maniera relativamente informale, per ora) l'apparente contraddizione con cui abbiamo aperto il post, la LTH si pone come una sorta di principio fondamentale da cui potremmo studiare più nel dettaglio il comportamento delle reti, attraverso l'idea dei tickets.
Prima di tutto, se i tickets sono la sola cosa che conta in una rete neurale, possiamo modificare il nostro processo di allenamento per focalizzarci quanto più possibile su di essi?
Nell'articolo gli autori esplorano questa ipotesi con una procedura piuttosto semplice:
- Inizializzare una rete neurale in maniera classica.
- Allenarla per un certo numero di epoche.
- Eliminare i pesi più ininfluenti (i più piccoli in valore assoluto).
- Resettare il resto dei pesi al valore del punto (1).
- Allenare nuovamente la rete rimanente.
- Eventualmente ripetere i punti (2)-(5).
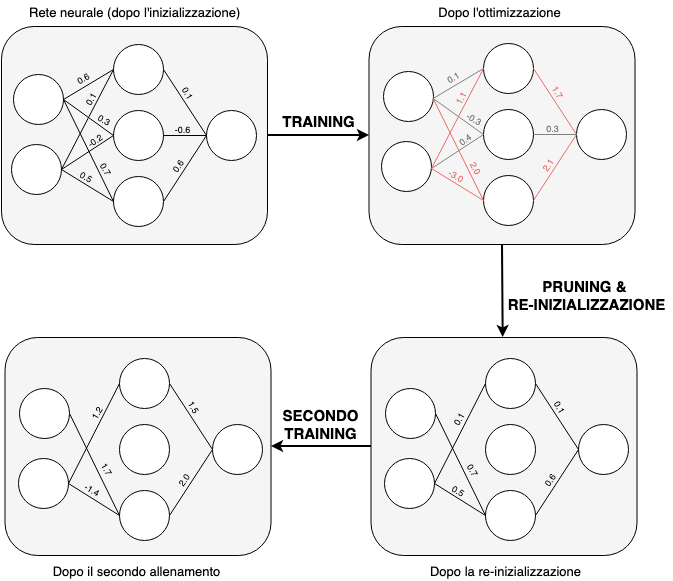
Un passaggio di questa procedura è mostrato nella figura che segue, dove abbiamo usato il rosso per evidenziare i pesi più significativi in seguito alla prima fase di allenamento. Il punto (4) è quello che sfrutta l'ipotesi: resettare i pesi al valore di inizializzazione è essenziale per non modificare l'eventuale 'ticket vincente'.

Su alcuni dataset di classificazione di immagini, questa procedura ottiene reti che sono fino al 90% più compatte di quelle di partenza. Alcuni lavori successivi degli stessi autori e di ricercatori di Uber hanno poi mostrato come estendere questa tecnica per renderla scalabile a reti e problemi più grandi.
Altrettanto interessante, un lavoro di alcuni ricercatori di Facebook ha mostrato come i ticket ottenuti siano in grado di generalizzare fra problemi diversi.
Conclusioni (per ora)
L'ipotesi descrive un meccanismo interessante sul funzionamento delle reti neurali e, soprattutto, permette di congetturare diversi filoni di ricerca e di esplorazione per capirne meglio i meccanismi, con una letteratura sul pruning di oltre trent'anni su cui basarsi.
Le domande fondamentali sono, ovviamente, se la congettura è vera e, in caso positivo, come progettare nuovi meccanismi per massimizzare la performance di questi ticket, migliorare l'inizializzazione delle reti, e molto altro.
Al tempo stesso, non tutti i ricercatori sono concordi sulla veracità della congettura (si vedano in particolare questo lavoro e questo articolo usciti in simultanea), ipotizzando che l'architettura di una rete, piuttosto che i singoli pesi all'inizializzazione, sia essenziale. Sicuramente, valutare l'importanza relativa di queste due congetture contrapposte sarà essenziale per migliorare la nostra comprensione delle reti neurali.
Se questo articolo ti è piaciuto e vuoi tenerti aggiornato sulle nostre attività, ricordati che l'iscrizione all'Italian Association for Machine Learning è gratuita! Puoi seguirci su Facebook, LinkedIn, e Twitter.