La magia della differenziazione automatica - Parte 1

Il calcolo automatico delle derivate è in assoluto "il cuore" di qualsiasi framework di deep learning. Esso permette di rendere completamente automatico (ed efficiente) uno dei meccanismi più complessi nell'uso di reti neurali, la back-propagation. Negli ultimi anni abbiamo visto la diffusione di strumenti di differenziazione automatica (autodiff) sempre più complessi e modulari, di pari passo con i progressi e successi del deep learning. Allo stesso tempo, nonostante la sua importanza, l'autodiff è un tema relativamente poco compreso. In questo tutorial spieghiamo come viene implementato con un piccolo esempio concreto, oltre a fare chiarezza su alcuni aspetti terminologici. Nella seconda parte del tutorial vedremo una implementazione in puro Python di un meccanismo di autodiff simile a quello reso celebre da PyTorch.

Partiamo da un esempio

Per rendere il tutorial più concreto possibile, supponiamo di avere questa espressione:

\[ f(w_1, w_2) = w1 \cdot \cos \left( 3w_1 + w_2 \right) \,. \]

$w_1$ e $w_2$ rappresentano due input della nostra funzione (es., due pesi della nostra rete neurale), mentre $f$ potrebbe rappresentare l'output della rete o una qualche funzione costo. Vogliamo calcolare (in automatico!) le derivate parziali di questa funzione (il suo gradiente) ovvero, in notazione matematica,

\[ \frac{\partial f}{\partial w_1} \;\;\text{ e }\;\; \frac{\partial f}{\partial w_2} \,. \]

Una minima conoscenza di analisi ci dice che questa operazione sembra abbastanza meccanica: è sufficiente conoscere le derivate delle funzioni elementari coinvolte (ad es., la derivata del coseno), e come queste si compongono tra loro in presenza di somme e prodotti. Qualsiasi framework di deep learning rende questa operazione di una semplicità disarmante. Ad esempio, in TensorFlow con la eager execution attiva potremmo scrivere:

import tensorflow as tf
import tensorflow.contrib.eager as tfe
tf.enable_eager_execution()

def f(w1, w2):
    return w1 * tf.cos(3*w1 + w2)

grad_f = tfe.gradients_function(f, ['w1', 'w2'])

Quello che si nasconde dietro questa operazione all'apparenza banale è ciò di cui parliamo nel resto del tutorial.

Un primo approccio: differenziazione numerica

Cominciamo dalle cose più semplici. Ad esempio, potrebbe stupirvi sapere che possiamo calcolare le nostre derivative in un paio di righe di codice, senza nessuna conoscenza aggiuntiva, semplicemente applicando alla lettera la definizione di derivata parziale (concentriamoci per ora solo sul primo argomento della funzione):

\[ \frac{\partial f}{\partial w_1} = \lim_{\delta \rightarrow 0} \frac{f(w_1+\delta, w_2) - f(w_1, w_2)}{\delta} \,. \]

Prendendo un $\delta$ molto piccolo otteniamo un'approssimazione di questa espressione alle differenze finite. Per esempio, per $w_1=2.0$, $w_2=1.5$ e $\delta=10^{-4}$ potremmo calcolare (con la funzione definita sopra):

dw1 = (f(2.0 + 1e-4, 1.5) - f(2.0, 1.5)) / 1e-4 # -5.2809715...,

ovvero una approssimazione corretta fino al secondo decimale.¹ Ci accorgiamo subito che questo metodo non ci porta molto lontano: oltre a dover calcolare nuovamente $f$ per ogni derivata parziale, dobbiamo anche tenere d'occhio tutti gli eventuali errori numerici che (per espressioni più complesse) possono diventare rapidamente significativi. Ciò nonostante, è sempre utile tenere a mente questo metodo, se non altro come check della corretta implementazione dei propri moduli (es., dalla guida di PyTorch: https://pytorch.org/docs/stable/autograd.html#numerical-gradient-checking).

Un passo avanti: differenziazione simbolica

Ritorniamo alla nostra idea di partenza: esprimendo la nostra $f$ in qualche linguaggio simbolico, possiamo applicare meccanicamente le regole della derivazione ed ottenere una seconda espressione, sempre simbolica, che rappresenta la derivata parziale rispetto ad un argomento. Questa è una metodologia che dovrebbe suonare molto familiare a chi di mestiere lavora con strumenti come MATLAB, Maple o WolframAlpha. Ad esempio, ecco uno screenshot di come potremmo ottenere la derivata parziale rispetto a $w_1$ nell'ultimo caso:

Ovvero:

\[ \frac{\partial f}{\partial w_1} = \cos(3w_1 + w_2) - 3w_1\sin(3w_1 + w_2) \,.\]

[Il calcolo è abbastanza semplice da replicare conoscendo la derivata del coseno, del prodotto di due funzioni, e della loro composizione, su cui torneremo tra pochissimo.]

Anche qui notiamo subito un dettaglio interessante: il valore su cui applichiamo il coseno ed il seno è lo stesso! In generale, ottenere un'espressione efficiente per via simbolica è un compito molto difficile, in quanto la grandezza dell'espressione della derivata può (nel caso peggiore) crescere esponenzialmente rispetto al numero di operazioni della funzione di partenza.

A causa di questo, praticamente nessun software di deep learning implementa questa tecnica.

Dalla differenziazione simbolica al grafo computazionale

Come fare per superare i limiti della differenziazione simbolica? L'idea di fondo è abbastanza sottile: dobbiamo vedere la formula da differenziare non come un'unica espressione simbolica, ma come una serie di operazioni elementari, in maniera equivalente ad una serie di istruzioni di codice in un qualsiasi linguaggio di programmazione. Applicando le regole delle derivate alle singole operazioni elementari di questo programma, possiamo ottenere un secondo programma (NON necessariamente un'espressione simbolica) che permette di calcolare numericamente le derivate. La spiegazione può sembrare confusionaria, ma diventerà tutto molto più chiaro con un esempio pratico.

Cominciamo con il riformulare la nostra espressione di partenza come una serie di operazioni elementari, in cui identifichiamo esplicitamente tutti i risultati intermedi.

\[ \begin{cases} w_1 = & \ldots \\ w_2 = & \ldots \\ z_1 = & 3w_1 \\ z_2 = & z_1 + w_2 \\ z_3 = & \cos(z_2) \\ z_4 = & w_1 z_3 \end{cases}\]

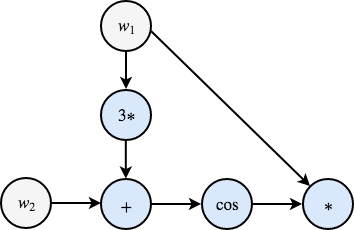
Così facendo, ci siamo avvicinati alla classica rappresentazione 'a grafo' a cui TensorFlow e simili ci hanno ampiamente abituato:

Il grafo esprime in maniera visiva (i) tutti i passi intermedi della nostra formula, e (ii) la dipendenza di ogni passo rispetto a quelli precedenti. Cosa farne?

Forward-mode automatic differentiation

L'idea fondamentale è che vogliamo associare ad ogni nodo del grafo un secondo valore, che rappresenti la derivata numerica di quel nodo rispetto ad uno degli input. Per comodità, nel seguito usiamo il nome $da$ per riferirci alla quantità $\frac{\partial a}{\partial w_1}$, ovvero la derivata della funzione $a$ rispetto a $w_1$. Ad esempio, $dz_2$ sarà la derivata di $z_2$ rispetto a $w_1$, mentre $dz_4$ sarà il valore cercato.

Proviamo a procedere per passi tenendo sempre bene a mente il grafo precedente:

1. Supponiamo di aver eseguito solo la nostra prima istruzione nel listato, ovvero l'assegnazione di un valore a $w_1$. Trivialmente abbiamo $dw_1 = 1$.
2. La seconda istruzione è l'assegnazione di $w_2$. Poiché $w_1$ e $w_2$ sono indipendenti, abbiamo $dw_2 = 0$.
3. Nel terzo passo moltiplichiamo $w_1$ per $3$: è immediato verificare che $dz_1 = 3$.
4. Nel quarto passo le cose si fanno interessanti: sommiamo a $z_1$ il valore di $w_2$. La derivata rispetto a $w_1$ è quindi la somma delle derivate dei due nodi precedenti: $dz_2 = dz_1 + dw_2 = dz_1 + 0 = dz_1$.
5. Al quinto passo applichiamo il coseno a $z_2$. Per la 'chain rule' della derivazione, abbiamo che $dz_3 = [\frac{\partial \cos(z_2)}{\partial z_2}]\cdot\frac{\partial z_2}{\partial w_1} = -\sin(z_2)dz_2$.
6. Il sesto passo è un prodotto di due termini. Usando la regola della derivata della moltiplicazione otteniamo: $dz_4 = z_3 + w_1dz_3$.

Al di là dei conti (che vi invitiamo a verificare), un aspetto dovrebbe essere apparente: ad ogni passo, i valori che andiamo a calcolare dipendono solo (a) dalla derivata elementare del singolo nodo (es., del coseno), e (b) dai valori calcolati nei nodi immediatamente precedenti sul grafo.

Grazie a quest'ultima proprietà, possiamo esprimere l'intera operazione come un listato di istruzioni molto simile a quello di prima:

\[ \begin{cases} dw_1 = & 1.0 \\ dw_2 = & 0.0 \\ dz_1 = & 3.0 \\ dz_2 = & dz_1 \\ dz_3 = & -\sin(z_2)dz_2 \\ dz_4 = & z_3 + w_1dz_3 \end{cases} \]

Possiamo interlacciare l'esecuzione di questa procedura con quella di partenza (es., calcolare $dz_3$ dopo $z_3$). Una volta conclusa l'intera procedura, $dz_4$ conterrà il valore che stavamo cercando!

Questo algoritmo per calcolare il gradiente viene detto forward-mode autodiff, ed i valori intermedi che abbiamo appena definito vengono detti dual numbers.²

Le buone notizie:

• Questo approccio è molto più efficiente della differenziazione simbolica (la complessità computazionale della procedura di derivazione è linearmente, e non più esponenzialmente, legata alla complessità della funzione di partenza).
• Il secondo punto è più sottile: poiché ora lavoriamo con istruzioni di programmazione (e non più con espressioni simboliche), possiamo combinare le istruzioni di partenza con altri costrutti di programmazione: cicli for, strutture dati, ed altri. Ad esempio, pensiamo ad un'operazione che inserisca una variabile in un dizionario: l'istruzione 'duale' sarà quella che estrarrà l'elemento dal dizionario, in maniera completamente trasparente all'utente. Se questo punto non vi è chiaro, non vi preoccupate, perché lo esploreremo con maggiore dettaglio nella seconda parte del tutorial.

Per riepilogare la differenza fra differenziazione automatica e simbolica, prendiamo in prestito una bella immagine da Wikipedia. Mentre la seconda lavora su un'espressione simbolica, la prima lavora sull'implementazione di questa espressione in un qualche linguaggio di programmazione:

Abbiamo finito? Purtroppo no! Anche se la nostra procedura è ora notevolmente più efficiente, abbiamo comunque bisogno di due procedure distinte per ciascun input: per calcolare la derivata rispetto a $w_2$ dobbiamo calcolare un insieme distinto di valori duali (seppur con molte ridondanze), inizializzando $dw_2$ ad 1.0, e $dw_1$ a 0. Una variante della forward-mode autodiff, che poi è quella usata da quasi tutti gli strumenti di deep learning, risponde a quest'ultima problematica.

Reverse-mode automatic differentiation

Il trucco finale sfrutta tutte le idee della sezione precedente, ma percorre il grafo "al contrario". Per farlo, dobbiamo introdurre un nuovo insieme di variabili intermedie, che questa volta descriveranno la derivata parziale di tutti i nodi del grafo rispetto all'output finale:

\[ ga = \frac{\partial a}{\partial z_4} \,.\]

Per calcolare queste nuove variabili dobbiamo ovviamente aspettare di aver raggiunto il nodo $z_4$: a questo punto possiamo seguire un ragionamento molto simile a quello di prima, ma percorrendo gli archi del grafo nella direzione opposta.

1. Cominciando dalla fine, abbiamo ovviamente $gz_4 = 1.0$.
2. Tornando indietro di uno step sul grafo: $gz_3$ è la derivata di $w_1z_3$ rispetto a $z_3$, ovvero $w_1$.
3. Arrivati a $z_2$, le cose diventano interamente speculari a quanto visto prima: per la chain rule, $gz_2$ è $\frac{\partial z_2}{\partial z_4} = \frac{\partial z_2}{\partial z_3}\frac{\partial z_3}{\partial z_4} = -\sin(z_2) gz_3$.
4. Con ragionamenti simili a prima, otteniamo poi $gz_1 = gz_2$ e $gw_2 = gz_2$.
5. L'ultimo caso è il più interessante: percorrendo all'indietro il grafo, $w_1$ riceve contributi da due 'rami' separati, i cui contributi si andranno a sommare: $gw_1 = 3gz_1 + z_3gz_4$.

Valgono regole esattamente speculari a quelle del forward-mode: il calcolo di ogni variabile temporanea richiede la conoscenza delle variabili temporanee di tutti i nodi successori sul grafo, oltre alle loro derivate elementari. Elencando il tutto come un listato di istruzioni:

\[ \begin{cases} gz_4 = & 1.0 \\ gz_3 = & w_1 \\ gz_2 = & -\sin(z_2) gz_3 \\ gz_1 = & gz_2 \\ gw_2 = & gz_2 \\ gw_1 = & 3gz_1 + z_3gz_4 \end{cases}\]

Nel reverse-mode possiamo calcolare tutte le derivate parziali degli input rispetto ad un singolo output con una sola iterazione, mentre abbiamo bisogno di più procedure per output separati: poiché in generale il numero di parametri di una rete neurale è molto grande, mentre abbiamo di solito un unico output (la funzione costo), questa modalità risulta infinitamente più efficiente, ed è lo standard in praticamente tutti i framework di deep learning! Ne vedremo un'implementazione concreta nella prossima parte del tutorial, in aggiunta ad alcuni dettagli pratici di grande interesse.

Letture di approfondimento

Per una breve introduzione più formale al tema, consigliamo un blog post del 2013 di Alexey Radul, Introduction to Automatic Differentiation. Un articolo scientifico estremamente chiaro e con molti più dettagli sulle tecniche (e sulla storia) dell'autodiff rimane Automatic Differentiation in Machine Learning: a Survey di Baydin et al.

Come discusso nell'articolo di Baydin et al., l'autodiff è in realtà un campo scientifico con numerosi decenni di storia, solo recentemente 'riscoperti' in parte dalla community del machine learning. Parte di questa storia e materiale si può ritrovare sul sito autodiff.org. Per una visione più variegata del settore nel contesto del machine learning, rimandiamo ai panel dell'Autodiff Workshop organizzato a NeurIPS 2017.

Se questo articolo ti è piaciuto e vuoi tenerti aggiornato sulle nostre attività, ricordati che l'iscrizione all'Italian Association for Machine Learning è gratuita! Puoi seguirci su Facebook, LinkedIn, e Twitter.

Note

Previous Post Next Post