La magia della differenziazione automatica - Parte 2

Nella prima puntata di questa serie abbiamo visto come funziona il calcolo delle derivate nei software di deep learning, e le differenze tra differenziazione simbolica, numerica, ed automatica. In questa seconda parte, passiamo ad una implementazione didattica in puro Python di un meccanismo di reverse-mode autodiff simile nell'interfaccia a quello reso celebre da PyTorch.

Un brevissimo recap

Qualsiasi libreria di deep learning ha la necessità di calcolare derivate parziali (gradienti) in maniera efficiente. La reverse-mode automatic differentiation (autodiff) è la tecnica più usata in pratica, e lavora salvando i risultati parziali dell'esecuzione del programma da differenziare, ed applicando in maniera furba la chain rule della derivazione "in senso inverso" rispetto all'esecuzione originale per calcolare i gradienti.

Ad esempio, riprendendo l'espressione di cui avevamo già discusso nella prima parte:

\[ f(w_1, w_2) = w1 \cdot \cos \left( 3w_1 + w_2 \right) \,. \]

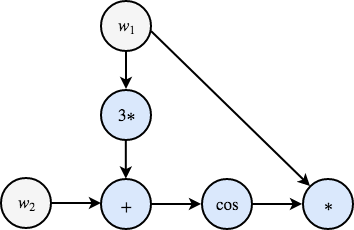
Come primo passo, possiamo riformulare l'espressione come una serie di operazioni elementari, esattamente come sarebbero poi eseguite in un compilatore/interprete:

\[ \begin{cases} w_1 = & \ldots \\ w_2 = & \ldots \\ z_1 = & 3w_1 \\ z_2 = & z_1 + w_2 \\ z_3 = & \cos(z_2) \\ z_4 = & w_1 z_3 \end{cases}\]

Per ogni variabile di input e variable intermedia $z_i$, definiamo una variabile duale che ne rappresenta la derivata parziale rispetto all'uscita, ovvero proprio i termini che ci interessano per ottimizzare espressioni di questo tipo con una discesa al gradiente:

\[ ga = \frac{\partial a}{\partial z_4} \,.\]

Seguendo i passi descritti nella prima parte, arriviamo ad un secondo insieme di istruzioni elementari che automatizzano il calcolo delle derivate:

\[ \begin{cases} gz_4 = & 1.0 \\ gz_3 = & w_1 \\ gz_2 = & -\sin(z_2) gz_3 \\ gz_1 = & gz_2 \\ gw_2 = & gz_2 \\ gw_1 = & 3gz_1 + z_3gz_4 \end{cases}\]

La domanda che ci poniamo ora è: come possiamo implementare questa procedura in un qualsiasi linguaggio di programmazione?

Autodiff in pratica: operator overloading

Concentriamoci su una singola operazione del nostro programma, ad esempio $z_3 = \cos(z_2)$. Nella fase di autodiff, seguiamo l'operazione in senso inverso, e questa operazione si traduce in un contributo al gradiente di $z_2$ dato da $-\sin(z_2) gz_3$, che dipende (a) dalla derivata del coseno ($-\sin$), e (b) dalla variabile duale $gz_3$ calcolata durante la fase di backward pass.

Le stesse considerazioni valgono per le altre operazioni. Ad esempio, l'assegnazione $z_2 = z_1 + w_2$ produce DUE contributi nella backward pass (poiché partecipano due variabili intermedie), $gz_1 = 1.0 * gz_2$ e $gw_2 = 1.0 * gz_2$, dove nuovamente abbiamo un contributo che viene dal nodo appena creato ($gz_2$), ed un contributo che deriva dalla derivata parziale della somma (in entrambi i casi, 1.0).

Il modo più semplice di implementare questa serie di operazioni è l'operator overloading. In sostanza, all'interno del linguaggio sostituiamo ogni operazione elementare (somma, seno, ...) con un operatore esteso che durante la sua valutazione:

1. Salva le variabili che hanno contribuito a quella espressione.
2. Salva le derivate parziali da usare come pesi nella fase backward (es., $-\sin(z_2)$ e $1.0$ negli esempi di prima).

Quando chiediamo le derivate rispetto ad un nodo, possiamo semplicemente seguire l'albero dell'espressione all'indietro, moltiplicando ogni volta per i pesi intermedi che ci siamo salvati (le frecce rosse negli schemi mostrati sopra).

Questo è il metodo in cui l'autodiff è implementato in praticamente qualsiasi libreria, da TensorFlow a PyTorch, ed è quello che seguiremo in questo tutorial.

Ci teniamo a sottolineare però che, nonostante la sua popolarità, questo non è l'unico modo di implementare la differenziazione automatica. Ad esempio Tangent, un altro progetto Google, lavora con un processo di source code transformation, andando ad elaborare direttamente il codice sorgente scritto in NumPy. Un approccio ancora più avanzato si ritrova in Swift for TensorFlow, nel quale questo procedimento diventa una componente fondamentale del linguaggio. Meccanismi di checkpointing permettono invece di alleviare il costo in memoria di tutte le variabili intermedie, a scapito di un maggior numero di calcoli richiesti.

Rimandiamo ad una report di C. Margossian per una panoramica più generale sull'implementazione dell'autodiff, che sicuramente subirà numerose evoluzioni con l'aumento dell'interesse sul tema.

Cosa facciamo in questo tutorial

Come detto all'inizio, andremo ad implementare un meccanismo didattico di reverse-mode autodiff, usando l'operator overloading. Per rendere le cose più semplici, consideriamo le seguenti semplificazioni:

• Solo scalari: l'estensione a vettori/matrici richiede qualche concetto aggiuntivo, e di gestire correttamente il meccanismo di broadcasting di NumPy.

• Poche operazioni: seguendo l'espressione di prima, andremo ad implementare solo addizioni, moltiplicazioni, ed il coseno. L'estensione ad altri operatori è però immediata.

• PyTorch-based: per quanto possibile, cercheremo di mantenere la terminologia e l'interfaccia di PyTorch per dare un'idea più chiara di come quello che facciamo si ritrova poi in un software reale.

Riguardo all'ultimo punto, se non avete mai usato PyTorch non vi preoccupate, in quanto sarà comunque tutto comprensibile anche a chi non hai mai avuto esperienza con PyTorch (ovviamente, vi invitiamo però a dare uno sguardo ai nostri tutorial).

Finalmente, l'implementazione

Riepilogando, ogni volta che eseguiamo una operazione, il meccanismo di autodiff deve tenere traccia dell'operazione e delle derivate parziali. Per semplificarci la vita, creiamo un wrapper per ogni singola variabile intermedia nella nostra espressione:

# A variable that traces its execution
class TracedVar:
    def __init__(self, data, requires_grad=False):
      # Grads will only be saved for requires_grad=True

      self.data = data                    # The actual value of the variable
      self.grad_fn = None                 # The parents of the variable
      self.grads = None                   # The computed gradient
      self.requires_grad = requires_grad  # Whether the gradient is saved or not

Segue una breve spiegazione di ciascun campo.

1. data è l'effettivo valore numerico dell'espressione.
2. grad_fn servirà a tenere traccia simultaneamente di quali variabili hanno contribuito all'espressione, e delle derivate parziali necessarie alla fase backward (vedi sotto).
3. grads servirà ad accumulare i gradienti nella fase backward (le variabili $ga$ di prima).
4. requires_grad permette di salvare i gradienti solo se espressamente richiesto (tipicamente, per i parametri del nostro modello neurale).

Aggiungiamo ora un primo operatore: il coseno.

def cos(x):
  z = TracedVar(np.cos(x.data))
  z.grad_fn = [
      (x, -np.sin(x.data)) # d(cos(x))/d(x) = -sin(x)
  ]
  return z

La prima riga calcola l'espressione, mentre la seconda salva i valori di cui abbiamo discusso prima: la variabile che ha generato l'espressione (x), e la derivata parziale del coseno.

L'implementazione della moltiplicazione è simile.

def _wrapped_mul(self, other):
    z = TracedVar(self.data * other.data)
    z.grad_fn = [
        (self, other.data),  # d(ab)/d(a) = b 
        (other, self.data)   # d(ab)/d(b) = a
    ]
    return z

L'unica differenza è che l'operazione di moltiplicazione ha due parenti (in questo caso chiamati self ed other), e per ciascuno di essi dobbiamo salvare la derivata parziale appropriata.

Per comodità, sovrascriviamo l'operatore $*$ della nostra classe TracedVar con la nostra nuova operazione (questo ci permette di scrivere operazioni del tipo a * b):

TracedVar.__mul__ = _wrapped_mul

L'addizione a questo punto è banale.

def _wrapped_add(self, other):
  z = TracedVar(self.data + other.data)
  z.grad_fn = [
      (self, 1.0),  # d(a+b)/d(a) = 1.0
      (other, 1.0)  # d(a+b)/d(b) = 1.0
  ]
  return z
TracedVar.__add__ = _wrapped_add

Arriviamo quindi al meccanismo di calcolo delle derivate. Copiando PyTorch, vogliamo calcolare le derivate parziali rispetto ad un oggetto TracedVar invocando backward(), ed accumulando le derivate richieste nei parametri grads di ciascuna variabile.

def backward(self, acc=1.0):

  if self.requires_grad:
    if self.grads is None:
      self.grads = acc
    else:
      self.grads += acc

  # Recursively compute gradients for parents
  if self.grad_fn is not None:
    [parent.backward(acc * weight) for (parent, weight) in self.grad_fn]

1. La variabile acc corrisponde al gradiente "propagato all'indietro" dall'algoritmo (le frecce rosse negli schemi di prima), e l'assegnazione 1.0 di default corrisponde alla riga $gz_4 = 1.0$ (la derivata dell'uscita rispetto all'uscita stessa è 1.0).

2. Se la variabile richiede di salvare il gradiente, questo viene accumulato nel parametro grads. Accumulare è essenziale in quanto una singola variabile potrebbe aver contribuito a più di una espressione.

3. Se la variabile non è un punto di partenza nel grafo (es., $w_1$ prima), propaghiamo il gradiente all'indietro per ogni parente, moltiplicandolo per il valore adeguato.

Testiamo la nostra implementazione

Definiamo l'espressione da cui siamo partiti:

w1 = TracedVar(2.0, requires_grad=True)
w2 = TracedVar(1.5, requires_grad=True)
v = TracedVar(3.0)
y = w1 * cos(v * w1 + w2)

Essendo l'esempio didattico, dobbiamo inserire nel nostro wrapper anche il valore costante 3.0 (di cui non vogliamo calcolare il gradiente), mentre in pratica questo potrebbe essere gestito con un meccanismo di casting automatico.

Grazie alla magia dell'operator overloading, l'espressione di y è indistinguibile da quella che avremmo scritto con gli operatori classici di Python, ma adesso capiamo che "dietro le quinte" accadono numerose operazioni aggiuntive interessanti.

Chiediamo il gradiente:

y.backward()

L'operazione non ritorna nulla, ma salva il gradiente all'interno di qualsiasi variabile per cui requires_grad=True:

w1.grads
>>> -5.2813645428134075

Possiamo valutare la correttezza dell'implementazione replicando a mano il gradiente:

w1_realgrad = np.cos(7.5) - 6.0*np.sin(7.5)
assert abs(w1.grads - w1_realgrad) <= 1e-15

Se questo articolo ti è piaciuto e vuoi tenerti aggiornato sulle nostre attività, ricordati che l'iscrizione all'Italian Association for Machine Learning è gratuita! Puoi seguirci su Facebook, LinkedIn, e Twitter.

Previous Post Next Post