Il Symbolic Aggregate approXimation (SAX) encoding è un metodo per semplificare le serie storiche. È stato inventato da Eamonn Keogh e Jessica Lin nel 2002. SAX è un modo di trasformare una serie temporale in una sequenza di simboli. L'idea di base è che ogni simbolo rappresenta un intervallo. Questa tecnica permette di condurre una dimensionality reduction sulle serie storiche, quindi possiamo considerarlo un metodo non supervisionato.
Bisogna evidenziare che il SAX è una tecnica molto robusta ai valori mancanti, e quindi utilizzabile quando si è in presenza di serie di lunghezza diversa.
Per rafforzare l'ultima considerazione vi invito a leggere un articolo di KDNuggets dove viene utilizzato SAX Encoding per trovare anomalie tra le stagioni di varie squadre di baseball. Non tutte le stagioni hanno lo stesso numero di match e alcuni dati sono mancanti.
Visto il momento in cui viene scritto questo articolo, proverò a utilizzare il SAX Encoding sui dati della protezione civile per cercare i pattern tra le serie regionali dei contagi da Covid-19.
- L'orizzonte temporale và dal 24/02/2020 al 21/04/2020.
- La distribuzione geografica è per Regione anche se il Trentino - Alto Adige è diviso nelle due province autonome.
La colonna che useremo sarà totale_positivi. Riporto direttamente dal README del repository ufficiale della protezione civile: Totale attualmente positivi (ospedalizzati + isolamento domiciliare).
Naturalmente non sono un medico/epidemiologo/virologo/... quindi il mio interesse è solo trovare un dataset che mi permettesse di spiegare come funziona l'algoritmo, non trarrò nessuna conclusione dai dati.
| data | denominazione_regione | totale_positivi |
|---|---|---|
| 2020-02-24T18:00:00 | Abruzzo | 0 |
| 2020-02-24T18:00:00 | Basilicata | 0 |
| ... | ... | ... |
| 2020-04-21T17:00:00 | Valle d'Aosta | 522 |
| 2020-04-21T17:00:00 | Veneto | 10077 |
Tutto il codice di questo articolo è disponibile su un notebook Google Colab. Il dataset aggiornato può essere scaricato qui.
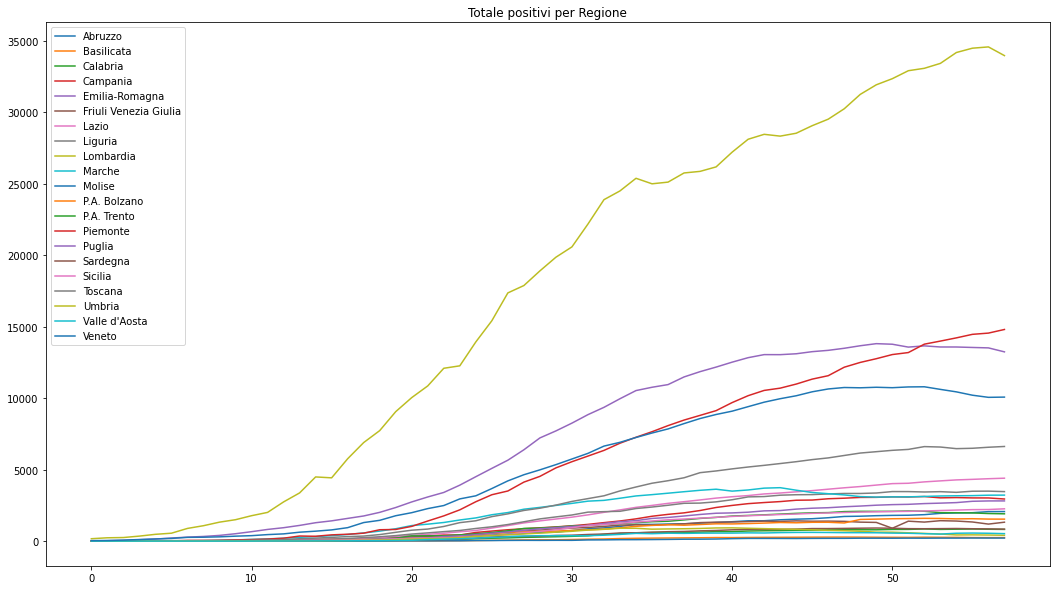
Per applicare questa tecnica bisogna avere la serie storica sulla riga e ad ogni colonna coinciderà uno step temporale.
| Regione | 1 | 2 | ... | 57 |
|---|---|---|---|---|
| Abruzzo | 0 | 0 | ... | 2067 |
| Basilicata | 0 | ... | ... | 245 |
| ... | ... | ... | ... | ... |
| Veneto | 32 | ... | ... | 10077 |
Le serie devono essere standardizzate così da avere la stessa scala.
\[ Z = \frac{x - \mu}{\sigma}\]
Questa tecnica non si basa solo sui volumi ma anche sugli andamenti. In questo caso in numeri assoluti la Lombardia è molto distante dalle altre regioni, ma lo sarà anche come andamento? Questa è la domanda a cui ci aiuterà a rispondere SAX Encoding.
tot_pos_pivot = totale_positivi.pivot(index="data", columns="denominazione_regione", values="totale_positivi").reset_index()
df_stand = ((tot_pos_pivot.drop("data", axis=1) - tot_pos_pivot.mean())/tot_pos_pivot.std()).TOra abbiamo la nostra matrice con sull'indice il nome della serie, ovvero la regione e sulle colonne il periodo da 0 a 57.
| Regione | 1 | 2 | ... | 57 |
|---|---|---|---|---|
| Abruzzo | -1.067762 | -1.067762 | ... | 1.699956 |
| Basilicata | -1.063952 | ... | ... | 1.041431 |
| ... | ... | ... | ... | ... |
| Veneto | -1.244880 | ... | ... | 10766 |
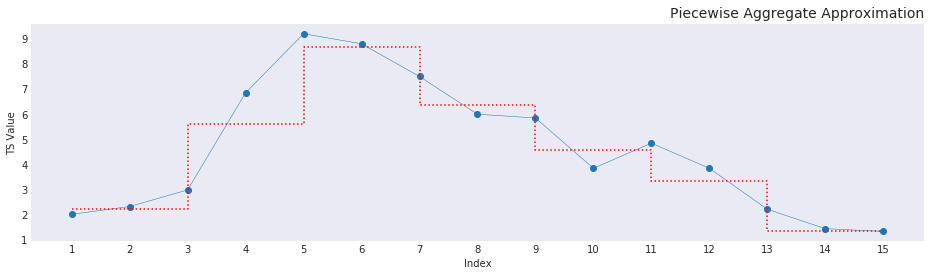
Come accennato inzialmente questo metodo riduce la dimensionalità della serie e lo fa proprio con la Piecewise Aggregate Approximation (PAA), l'idea alla base è "riassumere" la sequenza in una serie di segmenti che ne riducano la lunghezza ma ne rappresentino ugualmente l'informazione.
Data una time series $Y =$ [$Y_{1}$, $Y_{2}$, ..., $Y_{n}$] che può essere ridotta in una sequenza $X =$ [$X_{1}$, $X_{2}$, ..., $X_{m}$] con $m \leq n$ l'equazione che sintetizza gli elementi della time series originale per adattarli alla nuova dimensione è la seguente:
\[ \bar{X}_i = \frac{m}{n} \cdot \sum_{j=n/N(i-1) + 1}^{(n/M)\cdot i} x_j\]
Quindi la media per ogni finestra temporale che costituirà la nuova sequenza. Si possono notare subito due casi particolari:
- $m = n$, la nuova sequenza è identica alla serie storica originale
- $m = 1$, la nuova sequenza ha un solo valore equivalente alla media dei valori dell'intera time series
Per applicare la P.A.A. avremo bisogno di scegliere la dimensione della finestra temporale su cui calcolare l'informazione, questo influirà anche su quanti segmenti verranno utilizzati per ricostruire la serie storica.
In questo caso, visto che i vari ragionamenti (sentiti in TV, ribadisco di non avere nessuna competenza) si basano su un tempo di 2 settimane, imposterò il parametro (window) $w=14$.
Ridimensionata, ogni serie sarà una sequenza di lunghezza_serie/w periodi, nella quale si prende la media del periodo come nuovo valore.
Attenzione: Bisogna impostare un controllo per non perdere informazioni, quindi se il nuovo numero di periodi non è un intero, esso và sempre arrotondato per eccesso.
windows = 14
new_len = int(np.ceil((df_stand.shape[1]/windows)))
# Crea il nuovo dataFrame
df_PAA = pd.DataFrame(index = df_stand.index, columns = range(0, new_len))
# Calcola la media di ogni window
ind = 0
for i in range(0,df_stand.shape[1], windows):
avg = df_stand.iloc[:,i:i+windows].mean(axis=1)
df_PAA[ind] = avg.values
ind +=1| denominazione_regione | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Abruzzo | -1.060876 | -0.785615 | 0.352059 | 1.252060 | 1.696609 |
| Basilicata | -1.055972 | -0.846662 | 0.516006 | 1.239693 | 1.028541 |
| Calabria | -1.088706 | -0.797959 | 0.449874 | 1.246324 | 1.333274 |
Preparato il dato si può lavorare a ciò che contraddistingue questa tecnica. Adesso il dato numerico verrà converito in stringa. La SAX String è derivazione del numero di livelli in cui si vuole suddividere la serie, ogni livello avrà un'etichetta, queste etichette verranno successivamente concatenate creando la SAX String. La scelta dei livelli influisce sul risultato, quindi bisognerebbe sempre farsi affiancare da un esperto di dominio, il consiglio è quello di non creare troppi livelli altrimenti si ha un'eterogeneità troppo alta e non si troverebbero pattern.
I livelli possono essere fissati oppure calcolati ad ogni periodo, in questo caso si preferisce la seconda opzione.
Non conoscendo il fenomeno, supporrò 3 livelli ["A", "B", "C"], e suddividerò i valori:
- dal minimo fino al primo quartile;
- tra primo e terzo quartile;
- superiore al terzo quartile.
In questi caso, potremmo interpretarli come:
- pochi contagi, ottima situazione;
- situazione nella media;
- grave emergenza.
Una volta definiti i livelli questi vengono concatenati in un'unica stringa detta appunto "SAX string", es. ABAAB.
# Sto ridondando con i DataFrame creati ma è per mostrare i vari step, sorry.
binned = pd.DataFrame(index = df_PAA.index, columns = df_PAA.columns)
for j in range(0, df_PAA.shape[1]):
bins = []
bins.append(df_PAA[j].min()-.01)
bins.append(df_PAA[j].quantile([0.25]).values[0])
bins.append(df_PAA[j].quantile([0.75]).values[0])
bins.append(df_PAA[j].max()+.01)
labels = ["A", "B", "C"]
binned[j] = pd.cut(df_PAA[j], bins, labels=labels)
binned['SAX_string'] = binned.apply(''.join, axis=1)Il risultato finale del SAX Encoding lo si può vedere in tabella.
| denominazione_regione | SAX_string |
|---|---|
| Abbruzzo | CAABC |
| Basilicata | CABBA |
| Calabria | BABBB |
| ... | ... |
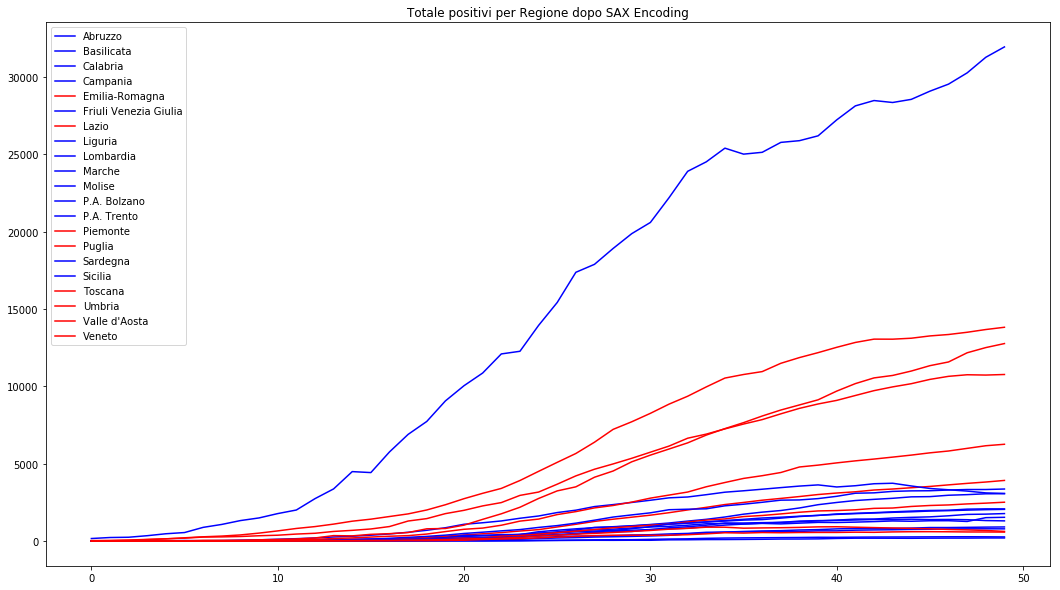
Il SAX Encoding può essere considerato un metodo non supervisionato di anomaly detection dove per anomalia (o outlier) non si intende la singola osservazione ma l'intera serie storica.
Possiamo calcolare la frequenza di ogni SAX String, impostato il limite che per noi determina un outlier etichettare come tale tutte le serie con frequenza della SAX String minore o uguale al bound.
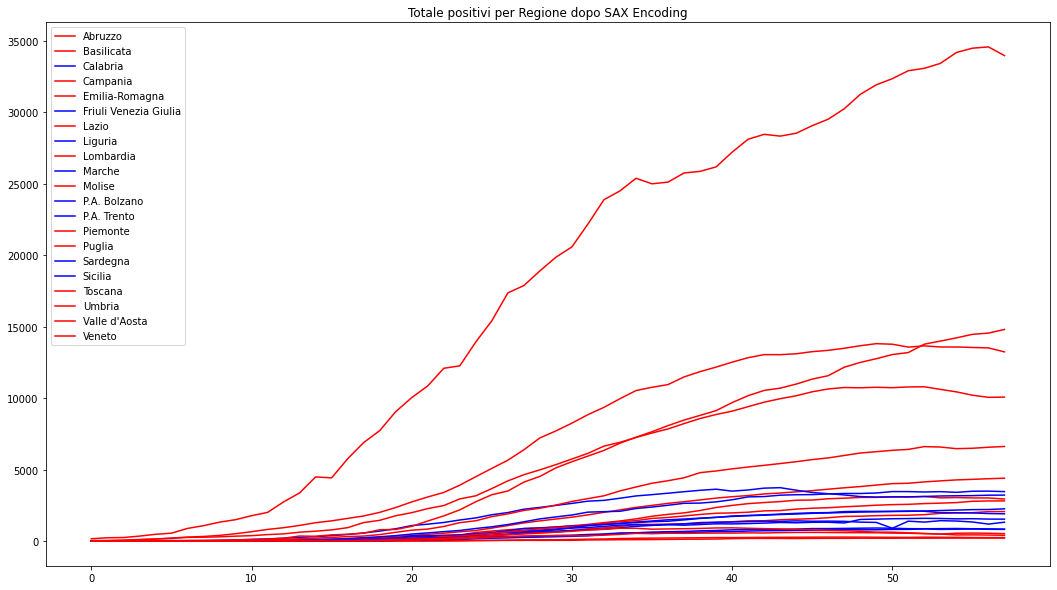
Nell'immagine ho impostato come bound 1.
In rosso abbiamo gli outlier, blu le sequenze con frequenza maggiore di 1, vediamo che quasi ogni regione ha un suo andamento, questo dovuto a diversi fattori (territorio, controlli, ...)
Sempre rimanendo nel campo dei modelli non supervisionati, le SAX String possono essere utilizzate per il clustering.
Un'applicazione che mi viene in mente è il clustering gerarchico utilizzando come misura di similarità (o dissimilarità a seconda se agglomerativo o divisivo) la distanza di Levenshtein.
Passando ai metodi supervisionati, avendo già delle serie storiche etichettate, penso ad esempio a quelle sul consumo energetico che hanno anche una certa stagionalità, si potrebbe applicare il KNN alla sequenza per classificare le nuove serie.
Nel precedente paragrafo ho citato la stagionalità perchè in questo articolo non è stato trattato un tema di forte interesse come il dato in stream. Con la diffusione dell'IoT le time series in stream sono un tema sempre più caldo sia per quanto riguarda l'immagazzinamento dei dati che per quanto riguarda le analisi.
Nel caso di serie con stagionalità, o forti componenti cicliche, oltre alla finestra temporale per la P.A.A. si potrebbe pensare ad una finestra per l'aggiornamento dei periodi con lo stesso timing dell'effetto. Ad esempio, se ho una serie con ciclicità mensile e voglio valutare i pattern su finestre settimanali potrei impostare:
- orizzonte di aggiornamento mensile;
- finestra per il SAX Encoding settimanale.
In questo modo sarebbe possibile studiare SAX String di lunghezza 4 o 5.
Naturalmente con fenomeni fortemente erratici questo è più complicato da decidere, quasi sicuramente i risultati dei nostri modelli (anomaly detection, classificazione, clustering, ...) varierebbero molto frequentemente.
Prendendo ad esempio il nostro dataset: se ci fermassimo una settimana prima, nel grafico seguente i dati si fermano al 13 aprile, le sequenze non singleton sarebbero molte di più. Questo solo per rimarcare ancora una volta l'importanza della scelta dela giusta finestra temporale e del periodo di osservazione in relazione al fenomeno che si và ad analizzare.
Se volete approfondire questo tema vi consiglio il paper "A Symbolic Representation of Time Series, with Implications for Streaming Algorithms" di Jessica Lin, Eamonn Keogh, Stefano Lonardi, Bill Chiu.
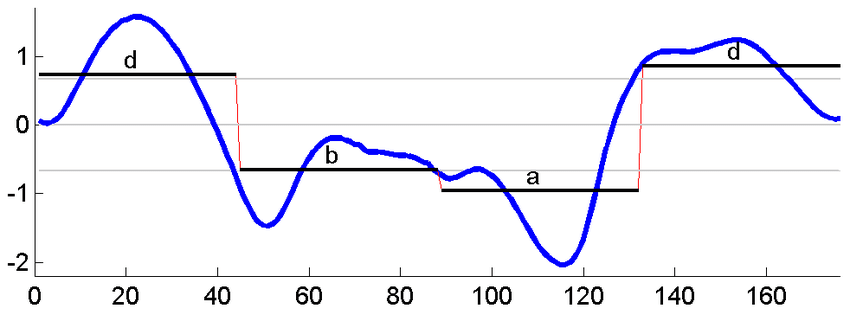
L'immagine di copertina è riadattata da (Yankov et al., 2007, Detecting time series motifs under uniform scaling, ACM SIGKDD).
Se questo articolo ti è piaciuto e vuoi tenerti aggiornato sulle nostre attività, ricordati che l'iscrizione all'Italian Association for Machine Learning è gratuita! Puoi seguirci su Facebook, LinkedIn, e Twitter.